Равномерный закон распределения на интервале
Равномерный и показательный законы распределения непрерывной случайной величины
Как было сказано ранее, примерами распределений вероятностей непрерывной случайной величины Х являются:
Дадим понятие равномерного и показательного законов распределения, формулы вероятности и числовые характеристики рассматриваемых функций.
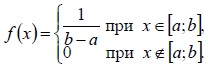
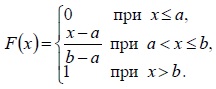
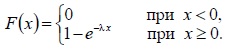
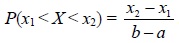
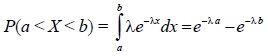
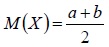
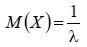
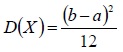
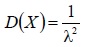
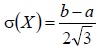
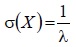
Примеры решения задач по теме «Равномерный и показательный законы распределения»
Автобусы идут строго по расписанию. Интервал движения 7 мин. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут; в) математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания пассажира.
Решение. 1. По условию задачи непрерывная случайная величина X= <время ожидания пассажира>равномерно распределена между приходами двух автобусов. Длина интервала распределения случайной величины Х равна b-a=7, где a=0, b=7.
2. Время ожидания будет менее двух минут, если случайная величина X попадает в интервал (5;7). Вероятность попадания в заданный интервал найдем по формуле: Р(х1 −λa − e −λb .
P(1 −5*1 − e −5*4 = e −5 − e −20 .
3. Вероятность того, что в результате испытания X ≥ 2 будем находить по формуле: P(a −λa − e −λb при a=2, b=∞.
Р(Х≥2) = P(1 −λ*2 − e −λ*∞ = e −2λ − e −∞ = e −2λ — 0 = e −10 (т.к. предел e −х при х стремящемся к ∞ равен нулю).
4. Находим для показательного распределения:
Другие статьи по данной теме:
- назад:Непрерывные случайные величины. Примеры решения задач
- далее:Нормальный закон распределения непрерывной случайной величины
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
- Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
- Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
- Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.
- Время ожидания автобуса, при условии, что пассажир приходит на остановку в случайный момент времени и автобусы ходят с постоянным интервалом.
- Ошибки при взвешивании.
- Ошибка округления числа до целочисленного значения. Очевидно, что такая случайная величина распределена равномерно на отрезке $\left[-0,5;0,5\right]$.
Список использованных источников
Равномерный закон распределения вероятностей
Пожалуй, равномерное распределение является самым простым из всех законов распределений непрерывных случайных величин. Непрерывная случайная величина $X$ является равномерно распределенной на отрезке $\left[a;b\right]$, если ее плотность распределения вероятностей имеет следующий вид:
Тогда соответствующая функция распределения имеет вид:
Графики функций плотности $f\left(x\right)$ и распределения $F\left(x\right)$ представлены на рисунке.
Для равномерного закона распределения числовые характеристики могут быть вычислены по известным формулам. Математическое ожидание:
Равномерно распределенная случайная величина $X$ принимает все свои значения лишь в конечном промежутке $\left[a;b\right]$, причем все эти значения случайной величины $X$ равновероятны. Примерами случайных величин, распределенных по равномерному закону, могут быть:
Пример 1. Плотность распределения вероятностей случайной величины $X$ имеет вид $f\left(x\right)=\left\<\begin
0,\ x\le 2\\
<<1>\over <5>>,\ 2 7
\end
Тогда математическое ожидание $M(X)=(a+b)/2=(2+7)/2=4,5$, дисперсия $D(X)=<\left(b-a\right)>^2/12=<\left(7-2\right)>^2/12=25/12\approx 2,083.$
Пример 2. Вычислить вероятность того, что при семи испытаниях менее трех раз случайная величина $X$ попадет в интервал $\left[0;1,5\right]$, если распределено по равномерному закону на отрезке $\left[0;6\right]$.
Запишем функцию распределения равномерно распределенной случайной величины $X\sim R\left[0;6\right]$.
Математическое ожидание равномерно распределенной случайной величины $X$ вычисляется по формуле:
Тогда вероятность того, что $X\in \left[0;1,5\right]$ равна разности значений функции распределения $F\left(x\right)$ на концах этого интервала: $P(0\le X\le 1,5)=F(1,5)-F(0)=1,5/6-0=0,25.$
Вероятность того, что при $n=7$ независимых испытаниях $X$ попадет в интервал $\left[0;1,5\right]$ менее трех раз, вычисляем по формуле: $P_7\left(k Да Нет
При копировании материала с сайта, обратная ссылка обязательна!
Функция НОРМРАСП
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
x — значение, для которого строится распределение.
Среднее — среднее арифметическое распределения.
Интегральная — логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
· Если аргумент «среднее» или « стандартное_откл » не является числом, функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!.
· Если стандартное_откл ≤ 0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!.
· Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
· Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
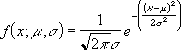
· Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x .
Функция НОРМСТРАСП
Возвращает стандартное нормальное интегральное распределение. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице. Данная функция используется вместо таблицы площадей стандартной нормальной кривой.
Z — значение, для которого строится распределение.
· Если z не является числом, функция НОРМСТРАСП возвращает значение ошибки #ЗНАЧ!.
· Уравнение плотности стандартного нормального распределения имеет следующий вид:
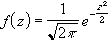
Функция НОРМОБР
Возвращает обратное нормальное распределение для указанного среднего и стандартного отклонения.
Вероятность — вероятность, соответствующая нормальному распределению.
Стандартное_откл — стандартное отклонение распределения.
· Если какой-либо из аргументов не является числом, функция НОРМОБР возвращает значение ошибки #ЗНАЧ!.
· Если вероятность 1, функция НОРМОБР возвращает значение ошибки #ЧИСЛО!.
· Если стандартное_откл ≤ 0, функция НОРМОБР возвращает значение ошибки #ЧИСЛО!.
· Если среднее = 0 и стандартное_откл = 1, функция НОРМОБР использует стандартное нормальное распределение (см. НОРМСТОБР).
Если задано значение вероятности, функция НОРМОБР ищет значение x , для которого функция НОРМРАСП( x , среднее, стандартное_откл , ИСТИНА) = вероятность. Однако точность функции НОРМОБР зависит от точности НОРМРАСП. В функции НОРМОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает значение ошибки #Н/Д.
Математика и информатика. Учебное пособие по всему курсу
Загрузить всю книгу 
5.3.3. Равномерный и нормальный законы распределения непрерывных случайных величин
На практике приходится при решении задач сталкиваться с различными распределениями непрерывных случайных величин. Плотность распределения f(x) непрерывной случайной величины называют законом распределения.
Следует рассмотреть некоторые важные для практики распределения случайных величин и соответствующие им числовые характеристики.
Непрерывная случайная величина X называется распределенной равномерно на отрезке [a,b], если её плотность распределения вероятностей постоянна на данном отрезке:
.
Функция распределения в этом случае согласно (5.7), примет вид:
.
1. Математическое ожидание по формуле (5.11):
.
.
Найти дисперсию и среднее квадратическое отклонение случайной величины X , равномерно распределенной на интервале (2;6).
.
.
Среднее квадратическое отклонение:
Это распределение реализуется, например, в экспериментах, в которых наудачу ставится точка на интервале [ a , b ], при этом случайная величина X – абсцисса поставленной точки.
Вероятность попадания равномерно распределенной непрерывной случайной величины Х на интервале [ a , b ], определяется по формуле (5.9а).
Примером равномерно распределенной непрерывной случайной величины Х является ошибка при округлении отсчета до ближайшего целого деления шкалы измерительного прибора, проградуированной в некоторых единицах.
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего деления. Найти вероятность того, что ошибка отсчета: а) превысит значение 0,04; б) меньше 0,04.
Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними делениями. Плотность равномерного распределения по формуле (5.14) равна:
,
где (b – a) – длина интервала, в котором заключены возможные значения Х.
Вне этого интервала f (x) = 0. В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,2. Поэтому плотность распределения вероятностей равна:
.
Тогда ошибка отсчета превысит значение 0,04, если она будет заключена в интервале (0,04; 0,2). По формуле (5.9а) вычисляется вероятность того, что при отсчете будет сделана ошибка превышающая значение 0,04:
.
Ошибка отсчета меньше 0,04 будет заключена в интервале (0; 0,04) с вероятностью:
.
Рис. 5.3. Плотность распределения вероятностей случайной величины, равномерно распределённой на отрезке [a;b]
Непрерывная случайная величина x имеет нормальльное распределение с параметрами: m, s > 0, если плотность распределения вероятностей имеет вид:
Равномерное распределение вероятностей
Простейшее из непрерывных распределений, с помощью которого моделируются многие реальные процессы. И самый такой распространённый пример – это график движения общественного транспорта. Предположим, что некий автобус (троллейбус / трамвай) ходит с интервалом в 10 минут, и вы в случайный момент времени подошли к остановке. Какова вероятность того, что автобус подойдёт в течение 1 минуты? Очевидно, 1/10-я. А вероятность того, что придётся ждать 4-5 минут? Тоже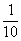 
. А вероятность того, что автобус придётся ждать более 9 минут? Одна десятая!
Рассмотрим некоторый конечный промежуток, пусть для определённости это будет отрезок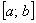 
. Если случайная величина 
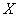обладает постоянной плотностью распределения вероятностей на данном отрезке и нулевой плотностью вне него, то говорят, что она распределена равномерно. При этом функция плотности будет строго определённой: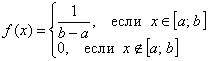 
И в самом деле, если длина отрезка (см. чертёж) составляет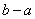 
, то значение 
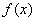неизбежно равно 
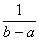– дабы получилась единичная площадь прямоугольника, и было соблюдено известное свойство: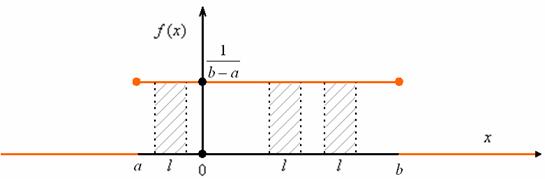 
Проверим его формально: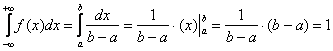 
, ч.т.п. С вероятностной точки зрения это означает, что случайная величина 
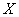достоверно примет одно из значений отрезка 
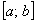…, эх, становлюсь потихоньку занудным старикашкой =)
Суть равномерности состоит в том, что какой бы внутренний промежуток фиксированной длины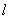 
мы ни рассмотрели (вспоминаем «автобусные» минуты) – вероятность того, что случайная величина 
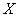примет значение из этого промежутка будет одной и той же. На чертеже я заштриховал троечку таких вероятностей – ещё раз заостряю внимание, что они определяются площадями, а не значениями функции 
!
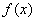Рассмотрим типовое задание:
Непрерывная случайная величина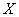 
задана своей плотностью распределения: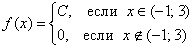 
Найти константу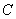 
, вычислить 
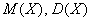и составить функцию распределения. Построить графики 
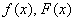. Найти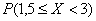 
Иными словами, всё, о чём только можно было мечтать 🙂
Решение: так как на интервале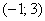 
(конечном промежутке) 
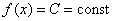, то случайная величина 
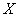имеет равномерное распределение, и значение «цэ» можно отыскать по прямой формуле 
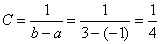. Но лучше общим способом – с помощью свойства: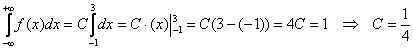 
…почему лучше? Чтобы не было лишних вопросов 😉
Таким образом, функция плотности: 
Выполним чертёж. Значения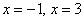 
невозможны, и поэтому жирные точки ставятся внизу: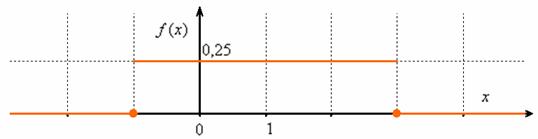 
В качестве экспресс-проверки вычислим площадь прямоугольника: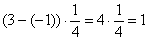 
, ч.т.п.
Найдём математическое ожидание, и, наверное, вы уже догадываетесь, чему оно равно. Вспоминаем «10-минутный» автобус: если случайным образом подходить к остановке много-много дней упаси, то в среднем его придётся ждать 5 минут.
Да, именно так – матожидание должно находиться ровно посерединке «событийного» промежутка: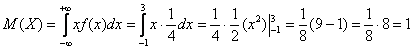 
, как и предполагалось.
Дисперсию вычислим по формуле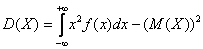 
. И вот тут нужен глаз да глаз при вычислении интеграла: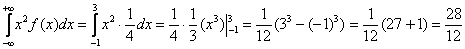 
Таким образом, дисперсия: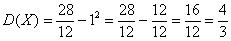 
Составим функцию распределения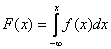 
. Здесь ничего нового:
1) если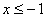 
, то 
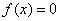и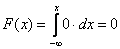 
;
2) если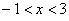 
, то 
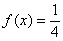и: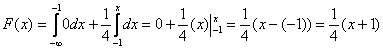 
3) и, наконец, при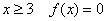 
, поэтому: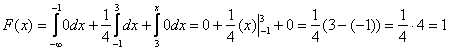 
В результате: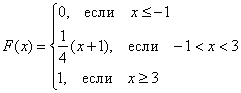 
Выполним чертёж: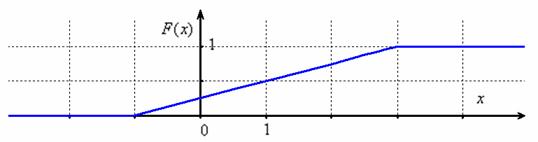 
На «живом» промежутке функция распределения растёт линейно, и это ещё один признак, что перед нами равномерно распределённая случайная величина. Ну, ещё бы, ведь производная линейной функции – есть константа.
Требуемую вероятность можно вычислить двумя способами, с помощью найденной функции распределения: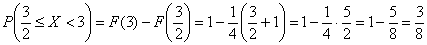 
либо с помощью определённого интеграла от плотности: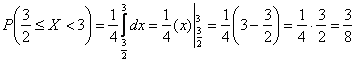 
Кому как нравится.
И здесь ещё можно записать ответ: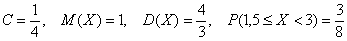 
, 
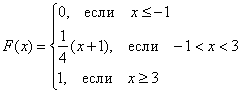, графики 
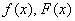построены по ходу решения.
…«можно», потому что за его отсутствие обычно не карают. Обычно 😉
Для вычисления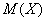 
и 
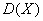равномерной случайной величины существуют специальные формулы, которые я предлагаю вам вывести самостоятельно:
Непрерывная случайная величина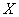 
задана плотностью 
.
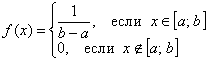Вычислить математическое ожидание и дисперсию. Результаты максимально упростить (формулы сокращённого умножения в помощь).
Полученные формулы удобно использовать для проверки, в частности, проверьте только что прорешанную задачу, подставив в них конкретные значения «а» и «б». Краткое решение внизу страницы.
И в заключение урока мы разберём парочку «текстовых» задач:
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Считая, что погрешности округлений распределены равномерно, найти вероятность того, что при очередном измерении она не превзойдёт 0,04.
Для лучшего понимания решения представим, что это какой-нибудь механический прибор со стрелкой, например, весы с ценой деления 0,2 кг, и нам предстоит взвесить кота в мешке. Но не в целях выяснить его упитанность – сейчас будет важно, ГДЕ между двумя соседними делениями остановится стрелка.
Рассмотрим случайную величину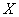 
– расстояние стрелки от ближайшего левого деления. Или от ближайшего правого, это не принципиально.
Составим функцию плотности распределения вероятностей:
1) Так как расстояние не может быть отрицательным, то на интервале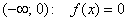 
. Логично.
2) Из условия следует, что стрелка весов с равной вероятностью может остановиться в любом месте между делениями*, включая сами деления, и поэтому на промежутке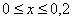 
:
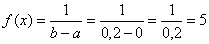
* Это существенное условие. Так, например, при взвешивании кусков ваты или килограммовых пачек соли равномерность будет соблюдаться на куда более узких промежутках.
3) И поскольку расстояние от БЛИЖАЙШЕГО левого деления не может быть больше, чем 0,2, то при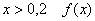 
тоже равна нулю.
Таким образом: 
Следует отметить, что о функции плотности нас никто не спрашивал, и её полное построения я привёл исключительно в познавательных цепях. При чистовом оформлении задачи достаточно записать только 2-й пункт.
Теперь ответим на вопрос задачи. Когда погрешность округления до ближайшего деления не превзойдёт 0,04? Это произойдёт тогда, когда стрелка остановится не далее чем на 0,04 от левого деления справа или не далее чем на 0,04 от правого деления слева. На чертеже я заштриховал соответствующие площади: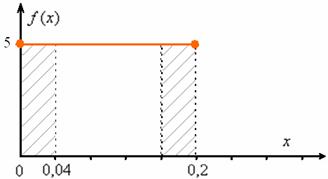 
Осталось найти эти площади с помощью интегралов. В принципе, их можно вычислить и «по-школьному» (как площади прямоугольников), но простота не всегда находит понимание 😉
По теореме сложения вероятностей несовместных событий: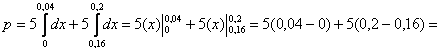 
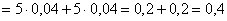– вероятность того, что ошибка округления не превзойдёт 0,04 (40 грамм для нашего примера)
Легко видеть, что максимально возможная погрешность округления составляет 0,1 (100 грамм) и поэтому вероятность того, что ошибка округления не превзойдёт 0,1 равна единице.
Ответ: 0,4
В других источниках информации встречаются альтернативные объяснения / оформление этой задачи, и я выбрал вариант, который показался мне наиболее понятным. Особое внимание нужно обратить на то, что в условии речь может идти о погрешностях НЕ округлений, а о случайных погрешностях измерений, которые, как правило (но не всегда), распределены по нормальному закону. Таким образом, всего лишь одно слово может в корне изменить решение! Будьте начеку и вникайте в смысл.
И коль скоро всё идёт по кругу, то ноги нас приносят на ту же автобусную остановку:
Автобусы некоторого маршрута идут строго по расписанию и интервалом 7 минут. Составить функцию плотности случайной величины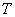 
– времени ожидании очередного автобуса пассажиром, который наудачу подошёл к остановке. Найти вероятность того, что он будет ждать автобус не более трёх минут. Найти функцию распределения 
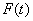и пояснить её содержательный смысл.
Несмотря на то, что время не может быть отрицательным, интервал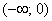 
не имеет особого смысла исключать из рассмотрения, ибо противоречия тут нет – вероятность того, что случайная величина 
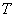примет невозможное значение, равно нулю.
Краткое решение и ответ в конце урока. Дополнительные задачи с равномерным распределением можно найти в тематическом решебнике.
И не успел никто опомниться, как подошёл очередной автобус, который отвезёт нас до остановки Показательное распределение и конечной под названием Нормальное распределение вероятностей.
Решения и ответы:
Пример 2. Решение: вычислим математическое ожидание: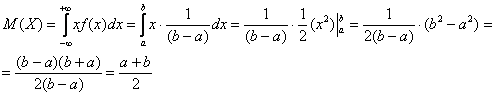 
Дисперсию вычислим по формуле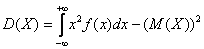 
. 
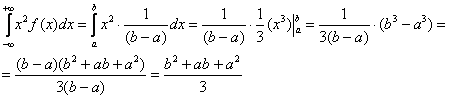
Таким образом: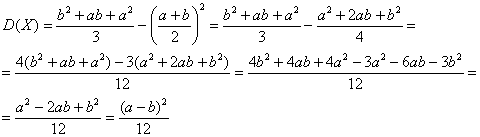 
Ответ: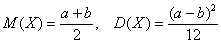 
Пример 4. Решение: случайная величина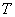 
имеет равномерное распределение с плотностью: 
Вычислим вероятность того, что пассажир будет ожидать автобус не более 3 минут: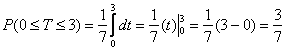 
Составим функцию распределения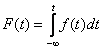 
:
1) если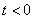 
, то 
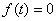и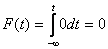 
;
2) если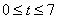 
, то 
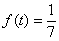и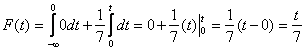 
;
3) если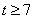 
, то 
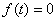, и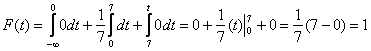 
.
Таким образом: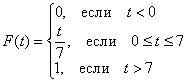 
Функция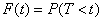 
описывает вероятность того, что пассажир дождётся очередной автобус за время, МЕНЬШЕЕ, чем 
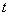. При увеличении 
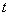от 0 до 7 эта вероятность линейно возрастает на 
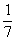в минуту и по достижению 
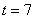достоверным становится тот факт, пассажир автобуса дождался.
Автор: Емелин Александр
(Переход на главную страницу)
Качественные работы без плагиата – Zaochnik.com
Равномерный закон распределения. Примеры
Целочисленных случайная величина Х имеет равномерный закон распределения, если вероятности ее возможных значений одинакова от эксперимента к эксперименту и вычисляются формуле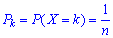 
В табличной форме записи равномерный закон распределения имеет вид: 
Условие нормировки для равномерного закона распределения имеет вид
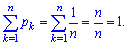
Вероятностная образующая функция на основе первой формулы принимает значение
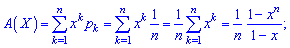
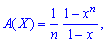
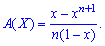
Числовые характеристики равномерного закона находим на основе образующей функции
1. Математическое ожидание находим по формуле
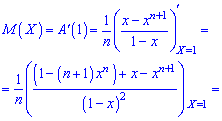
При х = 1 получаем неопределенность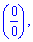 
которую раскрываем по правилу Лопиталя
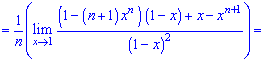
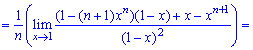
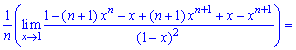
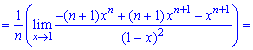
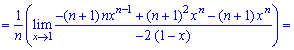
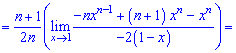
При х = 1 нова имеем неопределенность вида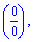 
которую также раскрываем по правилу Лопиталя
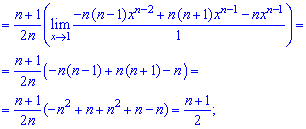
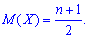
Вычисление заняли богатая времени, однако формула для математического ожидания получилась довольно легкой.
2. Выполнив подобные, но более громоздкие преобразования, дисперсию и среднее математическое отклонение находим по формулам
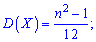
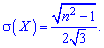
3. Для равномерного распределения вероятностей асимметрия и эксцесс равны нулю
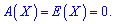
Есть и другое определение, согласно которому функция имеет равномерное распределение, если некотором интервале плотность вероятностей принимает постоянное значение
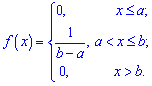
Функция распределения вероятностей для равномерного закона определяется интегрированием
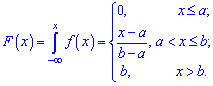
Математическое ожидание в таких случаях определяют зависимости
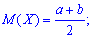
дисперсию по формуле
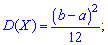
и среднее квадратическое отклонение через корень
Вероятность попадания случайной величины Х в некоторый интервал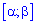 
, содержащийся внутри интервала 
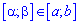определяется по формуле
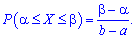
Приведенные формулы часто являются применимыми на практике чем те, которые были даны выше.
Рассмотрим примеры отыскания числовых характеристик.
Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение М (Х), D (X), S (Х), Найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х имеет равномерный закон распределения и возможные значения ее значение лежит в диапазоне 1..50:
.
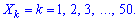Решение. По условию задачи имеем следующие данные n = 50, p = 1/50=0,02.
Согласно формулам вычисляем математическое ожидание
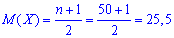
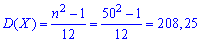
среднее квадратическое отклонение
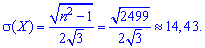
Пример 2. Поезда в метро прибывают на станцию ??каждые 10 минут. Определить вероятность того, что время ожидания состава не будет больше 4 минуты.
Решение. По условию задачи имеем два интервала
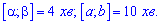
Согласно формуле, искомая вероятность равна доле этих величин
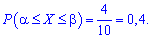
Задачи на отыскание интервала попадания случайной величины, распределена по ривнимирним законом решайте по такой же схеме. Она проста и не требует сложных вычислений.
Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / Ответы на вопросы по теории вероятности прошлых лет / 19.Равномерный закон распределения
19. Равномерный закон распределения и его числовые характеристики.
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).
Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероятности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.
Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:
Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.
Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1(исходя из св-в плотности вероятности ), то
Таким образом, непрерывная случайная величина X имеет равномерный закон распределения, на отрезке [a, b], если её плотность вероятности
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:
Теорема. Функция распределения случайной величины X, распределённой по равномерному закону, есть
её математическое ожидание 
а её дисперсия 
Графики функций f(x) и F(x) имеют вид:
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке [-0,5; 0,5]), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению. Так, случайная величина X, распределённая равномерно на отрезке [0; 1], называемая «случайным числом от 0 до 1», служит исходным материалом для получения случайных величин с любым законом распределения.
Найдем числовые характеристики.
Используя формулу для вычисления математического ожидания НСВ, имеем:
Таким образом, математическое ожидание случайной величины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.
Найдем дисперсию равномерно распределенной случайной величины:
откуда сразу же следует, что среднее квадратическое отклонение:
Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]:
Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.
Пример1. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке. Будет ожидать очередной автобус менее 3 минут.
СВ- время ожидания автобуса имеет равномерное распределение. Тогда искомая вероятность будет равна: 
Пример2. Ребро куба х измерено приближенно. Причем 
Рассматривая ребро куба как случайную величину, распределенную равномерно в интервале (a, b), найти математическое ожидание и дисперсию объема куба.
Объем куба- случайная величина, определяемая выражением У= Х3. Тогда математическое ожидание равно: