Применение нормальный закон распределения

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.

История применения закона нормального распределения в социальных и биоло­гических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как про­должительность жизни, возраст вступления в брак и появления первого ребенка и т. д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встре­чаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые от­клонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины». В его исследованиях, и позднее — в исследованиях англичанина Ф. Галь-тона, было доказано, что распределение частот встречаемости любого демографиче­ского (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколо-

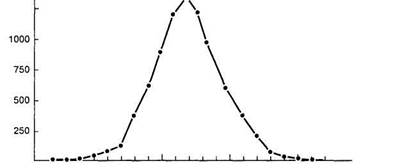
152 165 178 191 РОСТ, CM

‘ Гласе Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976. С. 98.

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

образную» форму (см. рис. 5.1). Форма таких распределений может быть описана ма­тематической формулой, которую предложил еще в XVIII веке математик де Муавр.

Де Муавр решал следующую задачу. Предположим, монета в азартной игре подбра­сывается 10 раз, и каждый раз она может с равным успехом выпасть «орлом» или «реш­кой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел», . 10 «орлов»? Сложные вычисления дают математически точное решение такой задачи (рис. 5.2). А если игра состоит из 100 подбрасываний монеты, или 1000? Де Муавру удалось доказать, что уравнение кривой, соединяющей вершины отрезков на рис. 5.2, для данного случая или для любой другой подобной задачи имеет следую­щую формулу:

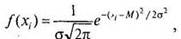
(5.1)

где/(х,) — высота подъема кривой, е — основание натурального логарифма (пример­но 2,718), л — число «пи» (примерно 3,14), Ми а — среднее и стандартное отклонения для переменной х„ которые определяют положение кривой на числовой оси и задают ее размах. Эта формула и соответствующая ей кривая (см. рис. 5.2) впоследствии по­лучили название закона нормального распределения.

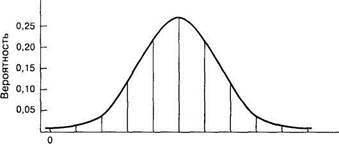
Рис. 5.2. График распределения вероятностей выпадения «орлов» в игре с 10 подбрасываниями монеты и кривая нормального распределения

ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК СТАНДАРТ

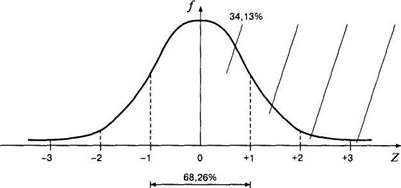
Последнее свойство объясняет название единичное нормальное распреде­ление и имеет исключительно важное значение. Благодаря этому свойству площадь под кривой интерпретируется как вероятность, или относительная частота. Действительно, вся площадь под кривой соответствует вероятности того, что признак примет любое значение из всего диапазона его изменчиво­сти (от -оо до +оо). Площадь под единичной нормальной кривой слева или справа от нулевой точки равна 0,5. Это соответствует тому, что половина ге­неральной совокупности имеет значение признака больше 0, а половина — меньше 0. Относительная частота встречаемости в генеральной совокупнос­ти значений признака в диапазоне от Z\ до Zi равна площади под кривой, ле­жащей между соответствующими точками. Отметим еще раз, что любое нор­мальное распределение может быть сведено к единичному нормальному распределению путем z-преобразования.

99,72%

Рис. 5.4. Стандартное нормальное распределение

П площадь между х, и х₂ в нормальном распределении со средним М_х и стандартным отклонением о равна площади между Z\ = (x_l — М_х)/а и Z2 = (x₂ — М_х)/а в единичном нормальном распределении.

Итак, наиболее важным общим свойством разных кривых нормального распределения является одинаковая доля площади под кривой между одни­ми и теми же двумя значениями признака, выраженными в единицах стан­дартного отклонения.

Полезно помнить, что для любого нормального распределения существу­ют следующие соответствия между диапазонами значений и площадью под кривой:

М±2осоответствует =95% (точно — 95,44%) площади;

М±3а соответствует =100%(точно — 99,72%) площади.

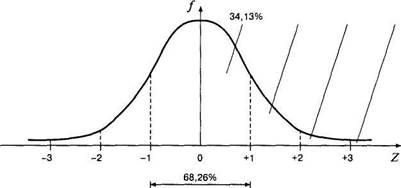
Единичное нормальное распределение устанавливает четкую взаимосвязь стандартного отклонения и относительного количества случаев в генераль­ной совокупности для любого нормального распределения. Например, зная свойства единичного нормального распределения, мы можем ответить на сле­дующие вопросы. Какая доля генеральной совокупности имеет выраженность свойства от — \о до +1о? Или какова вероятность того, что случайно выбран­ный представитель генеральной совокупности будет иметь выраженность свойства, на За превышающую среднее значение? В первом случае ответом будет 68,26% всей генеральной совокупности, так как от — 1 до +1 содержится 0,6826 площади единичного нормального распределения. Во втором случае ответ: (100-99,72)/2 = 0,14%.

Полезно знать, что если распределение является нормальным, то:

90%всех случаев располагается в диапазоне значений М+ 1,64а;

99%всех случаев располагается в диапазоне значений М+ 2,58с.

Существует специальная таблица, позволяющая определять площадь под кривой справа от любого положительного z (приложение 1). Пользуясь ею, можно определить вероятность встречаемости значений признака из любого диапазона. Это широко используется при интерпретации данных тестирования.

Основные законы распределения случайных величин

Нормальное распределение

Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и а, если ее плотность вероятности /(*) имеет вид

(2.20)

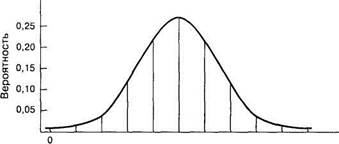
Кривая нормального распределения /(*) (нормальная кривая, или кривая Гаусса) приведена на рис. 2.1.

Нормальный закон распределения случайной величины с параметрами а = 0 и а = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Математическое ожидание случайной величины X, распределенной по нормальному закону, равно параметру а этого закона, а ее дисперсия – квадрату параметра σ, т. е.

Рис. 2.1. Кривая нормального распределения

Наиболее важные свойства случайной величины, распределенной

по нормальному закону:

1. Вероятность попадания случайной величины в интервал

(2.21)

где

2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания а не превысит по абсолютной величине величину‘, равна:

(2.22)

где

3. «Правило трех сигм». Если случайная величина X распределена нормально (с параметрами а и ст), то практически достоверно, что абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е.

(2.23)

4. Если случайная величина X имеет нормальный закон распределения с параметрами а и, то практически достоверно, что ее значения заключены в интервале

5. Коэффициент асимметрии и эксцесс нормально распределенной случайной величины равны нулю [18].

Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях.

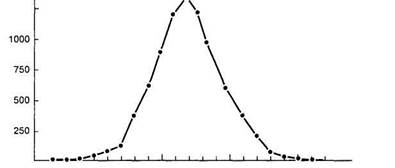
Рис. 5.1. Полигон частот для роста 8585 взрослых людей, родившихся в Англии в XIX в. 1

‘ Гласе Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976. С. 98.

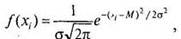
Итак, исход азартной игры, и продолжительность жизни, и рост человека — все это случайные события, частота (или вероятность) встречаемости которых подчинена закону нормального распределения. А. Кетле объяснял это существованием «идеала» человеческой природы, которому соответствуют средние значения различных пока-

зателей. Ф. Гальтон, двоюродный брат Ч.Дарвина, проявление нормального закона рассматривал в связи с биологической изменчивостью, наследственностью и отбором. В дальнейшем трудами Ф. Гальтона и его последователей было доказано, что и психо­логические особенности, например способности, подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистичес­кого аппарата проверки гипотез происходило на базе этого общего закона.

Подведем важный итог этого краткого исторического экскурса. Начиная со второй половины XIX столетия измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа. Если инди­видуальная изменчивость некоторого свойства есть следствие действия мно­жества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения.

Закон нормального распределения имеет целый ряд очень важных след­ствий, к которым мы не раз еще будем обращаться. Сейчас же отметим, что если при изучении некоторого свойства мы произвели его измерение на вы­борке испытуемых и получили отличающееся от нормального распределение, то это значит, что либо выборка нерепрезентативна генеральной совокупно­сти, либо измерения произведены не в шкале равных интервалов.

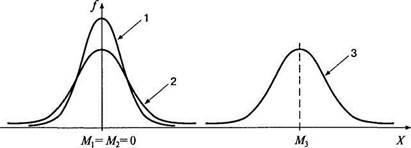
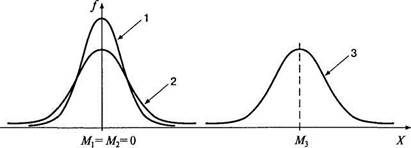
Каждому психологическому (или шире — биологическому) свойству соот­ветствует свое распределение в генеральной совокупности. Чаще всего оно является нормальным и характеризуется своими параметрами: средним (М) и стандартным отклонением (о). Только эти два значения отличают друг от дру­га бесконечное множество нормальных кривых, одинаковой формы, задан­ной уравнением (5.1). Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандар­тное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения (рис. 5.3).

Все многообразие нормальных распределений может быть сведено к од­ной кривой, если применить ^-преобразование (по формуле 4.8) ко всем воз­можным измерениям свойств. Тогда каждое свойство будет иметь среднее 0 и стандартное отклонение 1. На рис. 5.4 построен график нормального распре­деления для М= 0 и а = 1. Это и есть единичное нормальное распределение, кото­рое используется как стандарт — эталон. Рассмотрим его важные свойства.

99,72%

Рис. 5.4. Стандартное нормальное распределение

□ если х, имеет нормальное распределение со средним М и стандартным отклонением о, то z = (х— М_х)/а характеризуется единичным нормаль­ным распределением со средним 0 и стандартным отклонением 1;

М±а соответствует«68% (точно — 68,26%) площади;

95%всех случаев располагается в диапазоне значений М± 1,96с;

Нормальный закон распределения — введение

Приветствую дорогих читателей и подписчиков блога statanaliz.info. Продолжаем разговор о распределении данных. Как мы знаем, распределение может быть эмпирическим и теоретическим. Эмпирические данные всегда ограничены своей точностью и охватом возможных ситуаций. Поэтому для расчета интересующих вероятностей, пределов отклонений, размеров выборок и т.д. используют теоретические модели распределения случайной величины.

Самая известная статистическо-вероятностная модель – это закон нормального распределения. Нормальный закон, как и другие теоретические распределения, не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. А вот конкретная форма распределения задается специальными параметрами в этом уравнении.

Например, всем понятно выражение типа у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Без заданных параметров невозможно четко представить эту линию. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами, которые «подгоняют» модель под реальные данные.

Нормальный закон в теории статистики имеет фундаментальное значение. Он также лежит в основе ряда других распределений, поэтому ухватить самую суть желательно сразу. Вначале, возможно, будет слегка мутновато, но потом станет значительно легче, обещаю. Фактически после знакомства с нормальным распределением откроются новые горизонты использования статистических методов. Кстати, собственное логическое мышление под действием статистики также начинает деформироваться, в результате чего, общение с творческими личностями превращается в испытание. Ну да ладно.

Начнем с истории. Рассказываю, как сам слышал. Возможно, где-то перепутаю века, царей или континенты. В общем, я ни разу не историк.

Краткая история открытия нормального закона

История нормального закона насчитывает уже почти 300 лет. Говорят, первым причастным к открытию стал гражданин Абрахам де Муавр, который зафиксировал свои соображения по этому поводу в далеком 1733 году. Речь тогда шла о теоретическом приближении биномиального распределения при большом количестве наблюдений. Однако труды математика не были оценены по достоинству и Абрахама несправедливо забывают, когда речь идет об открытии нормального распределения. Широкое признание нормальный закон получил благодаря анализу выборочных данных.

Сейчас всем известно, что результаты выборочного исследования всегда ошибочны относительно истинного значения, которое исследователь и пытается оценить с помощью выборки. Если провести несколько измерений, то все они, скорее всего, будут отличаться друг от друга и, соответственно, от оцениваемого показателя по генеральной совокупности.

Статистика – наука исключительно практическая. Точность выводов здесь не пустой звук, а одна из насущных задач. В то же время вариация данных не способствует решению проблемы. Например, астрономы, проводя одни и те же наблюдения за небесными телами, все время получали различные результаты. Поначалу они считали, что всему виной их собственная небрежность и старались этот факт не сильно афишировать. Однако вопрос о постоянных отклонениях торчал занозой в ученом месте и не давал покоя пытливым умам тогдашних математиков. Как же быть с тем обстоятельством, что фактически нет возможности получить однозначный результат измерений? Что делать? Куда бежать? И какой из этого следует вывод? (последний вопрос от Ослика Иа).

И вот, эволюция мысли докатилась до того, что в светлую голову гражданина по имени Даниил Бернулли пришла замечательная мысль: разброс данных у самых различных явлений имеет что-то общее. Так, он сравнил разброс отклонений в астрономических наблюдениях с разбросом попаданий лучника в мишень и обнаружил, что и там и там максимальная концентрация результатов приходится на область относительно близкую к среднему значению, в то время как значительные отклонения происходят гораздо реже. Даниил подумал: а с чего бы это? И развивая успех, предложил соответствующий математический закон. Однако на этот раз ему не фартануло – закон оказался неверным. Кстати, этот Даниил был племянником другого Бернулли по имени Якоб. Того самого, который придумал закон больших чисел и процесс своего имени (когда в некотором эксперименте имеют место только два возможных исхода: благоприятный и неблагоприятный).

Тем не менее, идея об универсальном распределении ошибок измерений не осталась не замеченной, и немного позже другие ученые все-таки сформулировали правильный закон о случайных отклонениях. К открытию стали причастны Карл Фридрих Гаусс и Пьер-Симон Лаплас.

Гаусс вывел закон о распределении ошибок, чем и увековечил память о себе названием соответствующей функции (1809 г.). Чуть позже (в 1812 г.) П. Лаплас получил интеграл, который сегодня известен как функция нормального распределения.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение. Центральная предельная теорема далее многократно уточнялась и видоизменялась, но суть ее осталась прежней. Таким образом, история открытия нормального закона насчитывает более 200 лет. Начиная от открытия Муавра, до окончательных формулировок ЦПТ в середине 20-го века. На сегодня мы имеем довольно развитый математический аппарат для анализа нормально распределенных данных.

На всякий случай еще раз отмечу, что приведенная выше история – это фривольный пересказ того, что я читал. Для серьезного изучения вопроса лучше обратиться к специализированной литературе.

Закон нормального распределения

Прежде чем погружаться в мир формул, крайне важно получить наглядное представление о предмете. Поэтому предлагаю начать с рисунка, с помощью которого далее будут изложены основные сведения о нормальном законе. Итак, функция плотности нормального распределения, она же функция Гаусса, имеет следующий вид.

Кривая Гаусса по форме несколько напоминает колокол, поэтому график нормального закона часто еще называют колоколообразной кривой. Если вдруг увидите термин «колоколообразная кривая», знайте, что речь идет о нормальном распределении.

Как видно, у графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Другими словами, вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины. Смотрим на картинку.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Теперь посмотрим на формулу, по которой нарисована колоколообразная кривая, т.е. на функцию Гаусса.

Выглядит немного пугающе, но сейчас разберемся. В функции плотности нормального распределения присутствует: две математические константы

π – соотношение длины окружности и его диаметра, равно примерно 3,142;

е – основание натурального логарифма, равно примерно 2,718;

два параметра, которые задают форму конкретной кривой

m — математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

ну и сама переменная x, для которой высчитывается значение функции, т.е. плотность вероятности.

Константы, понятное дело, не меняются. Зато параметры — это то, что придает окончательный вид конкретному нормальному распределению. Отсюда и название: параметрическая функция или семейство параметрических функций. Напомню, есть и другие теоретические распределения, но мы сейчас говорим о нормальном.

Итак, конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности, что хорошо видно на самодвижущейся картинке.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса сконцентрирована у центра. Если же у данных большой разброс, то они «размажутся» по широкому диапазону.

Плотность нормального распределения не имеет прямого практического применения (если не считать приближенных расчетов при использовании биномиального распределения). Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя свойство непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

Применение нормальный закон распределения

Закон нормального распределения, или как его еще называют – кривая Гаусса, является одним из основных столпов в теории вероятности. Его применение можно проследить практически во всех сферах современного человеческого знания, от физики до философии. Я же попробую в кратком обзоре на примерах, объяснить как можно применить этот принцип, при аналитике народных процессов в социологии.

Хотя точное вычисление кривой Гаусса и требует решения довольно сложного уравнения, в этом тексте знания высшей математики вам не потребуются. И так, давайте для начала поймем, в общих чертах, в чем смысл этого графика, на примере изображения, показанного в заголовке статьи. Закон нормального распределения показывает вероятность некоторого значения из некоторой градации этих самых значений. Ось X является цифровым представлением этой самой градации и уходит от нуля в обе стороны до относительной бесконечности (но в некоторых случая она жестка ограничена). Ось Y является показателем величины вероятности значения из градации и может быть от нуля до одного. Сложно? Нет, все просто, взгляните вот на этот график и вам станет все довольно ясно.

Допустим, вы идете по улице, хотите спросить что-то умное у прохожего, и обращаясь к случайному человеку, вы можете быть уверены в том, что с максимально вероятностью он будет человеком среднего ума, в меньшей вероятности, что он будет дураком или умником и в практически минимальной возможности – гением или откровенным тупицей.

Одним словом этот график показывает вероятностное распределение интеллектуальности общества. Таким образом, обратившись к любой позиции на графике, можно сказать, какова вероятность при переборе людей, встретить гения, умного или дурака.

Естественно этот график является просто примером, и может не иметь никакого отношения к реальности. Для реальной же картины подобного рода, должен работать целый статистический комитет. Как можно понять из приведенного примера, график может деформироваться, в ту или иную сторону, и представлять уже иную вероятность. Показанный же график, называется – Стандартным нормальным распределением, потому что такая форма кривой вероятности установлена самой природой. И если мы обратимся в мир биосферы, и будем оценивать разные вероятности, то обнаружим, что данная форма кривой будут доминировать.

В определении ЗНР я указал, что ось X уходит по обе стороны в бесконечность. Дело в том, что оценка, каких либо общественных величин методом живой статистики, является явлением, находящемся только в настоящем времени. Общество не стоит на месте, оно постоянно движется, развивается или деградирует, поэтому сейчас оно одно, завтра другое, а значит, будет и другая форма и положение кривой Гаусса. Если не уходить с позиции стандартного нормального распределения, то для демонстрации вышесказанного можно опереться на ту же кривую вероятности интеллектуальной развитости общества.

График представляет собой пример оценки интеллектуального развития общества за некоторый необъявленный промежуток времени. Зеленая кривая, находящаяся на нуле, показывает положение дел «раньше». Красная и синяя кривые показывают момент «сейчас». Две кривые (красная и синяя) показаны исключительно в качестве иллюстрации, так как в реальной ситуации будет только одна из них, ведь общество не может одновременно развиться и деградировать по одному и тому же критерию оценки. Разбор одной из кривых, например красной, покажет вот такую картину. Общество поумнело на две единицы градации, что стало причиной того, что те люди, которые раньше считались очень умными, стали обычным явлением, те, кого раньше считали гениями, стали частенько встречаться и уже не являются чем-то необычным, а не очень умные в былые времена люди стали считаться чуть ли не дегенератами. Полностью противоположная картина будет при оценке синей кривой. Ее кстати очень хорошо продемонстрировал фильм «Идиократия», в котором «человек со средним умом» попав в будущее, оказался умнейшим человеком на земле, потому что за столетия, общество умственно деградировало настолько, что уровень дегенерата в нем стал среднестатистическим.

На основе понимания и умения выстраивать эти графики, можно не только оценивать движение общества в прошлом, но и строить планы на будущее на основе осознания того, как должно быть. Например, усиленно рассматриваемую мной в последнее время проблему алкоголизации общества, можно привести вот в такой форме. (Это чисто мое субъективное мнение, сформированное не математической статистикой, а тем, что я лично вижу вокруг себя.)

Тут присутствует жесткое ограничение оси X , за пределами которого, толкование кривой становится бессмысленно. На приведенном графике я определил четкие границы рассматриваемого явления – от идейного трезвенника до запойного алкоголика. Ясно, что попытка оценить точку кривой за этим диапазоном невозможна, из-за отсутствия величины оценки. В умственном развитии, конечно, тоже есть границы диапазона, но правда такова, что он настолько велик, что проще определить его как бесконечность, нежели как ограниченную величину. Так же на графике видна деформация одной из кривых, что является естественным положением дел в отношении описываемого явления.

И так, на графике красной кривой, показано приблизительное положение дел с алкоголизацией Российского общества на данный момент времени. Зеленой линией демонстрируется положение вещей с употреблением алкоголя «как должно быть» в нормальном (здоровом и думающем) обществе. Таким образом, мы видим, очень печальное положение вещей в данный момент. Если начать перебирать людей поштучно, мы выясним, что наиболее часто среди них будут встречаться пассивные алкоголики (термин определенный мной в прошлой статье «Алкогольная арифметика с картинками», обозначающий человека регулярно (через день, раз в неделю, раз в месяц, неважно, важно то, что ему это нравиться и он на этом сидит) выпивающего независимо от количества выпиваемого). Приблизительно с равной вероятностью будут встречаться позволяющий себе выпить (т. е. равнодушные – предложат, выпьет, не предложат не будет) и алкоголики. С еще чуть меньшей вероятностью – совсем падшие и запойные алкоголики. Трезвенник при таком положение вещей — откровенный рецидив, а идейный трезвенник, так вообще явление крайне редкое. (Идейный трезвенник – человек который не просто ведет трезвый образ жизни, а несет при этом некую идеологию, например, прямо заявляет о принципах здорового общества.)

В нормальном же обществе (зеленая кривая), трезвенник должен быть нормой. С минимальным отрывом от него должен идти идейный трезвенник. А вот равнодушный человек, позволяющий не отказаться от рюмочки, уходит в область рецидива, и становиться чуть ли не врагом общества. Пассивных алкоголиков как вы понимаете в том обществе вообще нет, так как они не смогут в нем существовать (они будут откровенными врагами народа, из-за того что понижают этику и демографию общества). Последнее как раз и выражено деформацией зеленой кривой Гаусса.

Ясное дело, что в этом крохотном тексте просто невозможно уложить всю полноту возможных вариантов применения закона нормального распределения в социологии. Но я надеюсь, что почву для размышлений я дал.

На мой взгляд, знанием данного закона, должен обладать любой человек, хотя бы чуть-чуть задумывающийся о своем будущем. А ведь, как известно – свое будущее, прямо зависит от будущего общества в целом, т. е. среды, в которой мы все живем. И если каждый будет знать, куда, а главное как нужно идти, то это уже гарантия уверенности, что мы идем к чему-то лучшему.

________________________________________ ________________________________________ ____

Большая Энциклопедия Нефти и Газа

Нормальный закон — распределение

Нормальный закон распределения полностью определяется двумя числовыми характеристиками — математическим ожиданием и дисперсией или средним квадрати-ческим отклонением. [1]

Нормальный закон распределения наблюдается в тех случаях, когда на признак явления действует много факторов, каждый из которых мало связан с большинством других, и влияние каждого фактора на конечный результат существенно меньше суммарного влияния всех остальных факторов. [2]

Нормальный закон распределения описывает поведение объектов, которым типичен износ, причем все отказы однородны по качеству и имеют малый разброс износа. [4]

Нормальный закон распределения наработки характерен для постепенного нарастания отказов, вызванных износом и старением. Он также применим при большом числе случайных факторов, когда влияние каждого из них незначительно по сравнению с совокупностью влияний остальных факторов. [5]

Нормальный закон распределения находит очень широкое применение в науке и технике. [6]

Нормальный закон распределения занимает особое место среди других законов распределения. [7]

Нормальный закон распределения ( часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает особое место среди других законов распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. [8]

Нормальный закон распределения находит также применение при анализе многих типов ошибок экспериментальных измерений и при оценке характеристик оборудования и систем. [9]

Нормальный закон распределения дает достаточно точные результаты при большом числе испытаний. При л 20 и при значениях Р, отличающихся от 0 и 1, полученные результаты нормального закона и биномиального распределения практически не отличаются. [10]

Нормальный закон распределения свободен от указанных недостатков биномиального распределения. И главное достоинство, что нормальный закон распространяется на очень большой класс случайных явлений и используется во многих практических случаях. [11]

Нормальный закон распределения , законы равной вероятности и треугольника применяются при практических расчетах размерных цепей наиболее часто. [12]

Нормальный закон распределения играет весьма важную роль в теории математической обработки результатов измерений и потому занимает среди других законов распределения особое место. Большинство встречающихся на практике случайных величин ( например, погрешности измерений) можегбыть представлено как сумма весьма большого числа сравнительно малых слагаемых, каждое из которых обусловлено действием отдельной причины, не зависящей от остальных. Теоретически и практически установлено, что такие суммы подчиняются ( в асимптотике) закону нормального распределения. [14]

Нормальный закон распределения наиболее часто встречается на практике. В силу важности этого закона мы изучим подробно его несколько позже. [15]

В электронной промышленности нормальному закону распределения подчиняется лишь часть измеряемых параметров технологических процессов и изделий. Функции распределения таких параметров, как обратные токи транзисторов и полупроводниковых диодов, а также ряд других параметров резко асимметричны. Это положение требует разработки соответствующих критериев оценки выборок. [c.160]

Применимость методов теории вероятностей в обработке промысловых данных в испытании основано на том, что возможные результаты всех измерений подчиняются нормальному закону распределения. [c.133]

Анализ промысловых данных испытания показывает, что наблюдающиеся распределения случайных ошибок измерения согласуются с нормальным законом распределения вероятностей. [c.133]

Оценки соответствия данных о рентабельности нормальному закону распределения приведены в табл. 8.1, оценки данных о темпах прироста — в табл. 8.2. Использованы [c.85]

Параметрический корреляционный анализ. Это наиболее распространенный и наиболее точный вид анализа, для которого разработано всестороннее вероятностное обоснование. Условием обоснованного применения параметрических методов анализа, как правило, является нормальный закон распределения данных, используемых для обработки. [c.86]

Основные оценки моделей. При выполнении регрессионного анализа нужно получить оценки, позволяющие оценить точность модели и вероятность ее существования. При нормальном законе распределения эти условия будут удовлетворены, если оценить [c.89]

Данные табл. 5.5 и рис. 5.1 показывают характерную для многих признаков форму распределения чаще встречаются значения средних интервалов признака, реже — крайние малые и большие значения признака. Форма этого распределения близка к рассматриваемому в курсе математической статистики закону нормального распределения. Великий русский математик А. М. Ляпунов (1857 — 1918) доказал, что нормальное распределение образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния. Случайное сочетание множества примерно равных факторов, влияющих на вариацию урожайности зерновых культур, как природных, так и агротехнических, экономических, создает близкое к нормальному закону распределения распределение хозяйств области по урожайности. [c.98]

Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Соотношение ст а зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором засоренности совокупности неоднородными с основной массой элементами чем это соотношение больше, тем сильнее подобная засоренность . Для нормального закона распределения а а 1,2. [c.106]

Полученное значение критерия %2 сравнивается с табличным при числе степеней свободы, равном числу групп (с условием Ф. Йей-тса), за минусом трех — по числу фиксированных параметров в формуле нормального закона распределения и с учетом равенства сумм теоретических и фактических частот (см. приложение, табл. 4). [c.200]

Несмотря на существенную условность применения в экономическом анализе стохастических моделей, они достаточно распространены, поскольку с их помощью можно прогнозировать динамику основных показателей, разрабатывать научно обоснованные нормативы, идентифицировать наиболее значимые факторы. Многие методы, разработанные в математической статистике, базируются на понятии нормального закона распределения, введенного Карлом Гауссом. Это обусловлено следующими причинами. Во-первых, оказывается, что при экспериментах и наблюдениях многие случайные величины имеют распределения, близкие к нормальному. Во-вторых, даже если распределение некоторой случайной величины не является нормальным, то ее можно преобразовать таким образом, чтобы распределение преобразования, т.е. новой величины, было уже близким к нормальному. В-третьих, нормальное распределение мо- [c.118]

Итак, для корректного использования методов математической статистики (например, корреляционно-регрессионного анализа) желательна проверка, хотя бы и достаточно формальная, основных предпосылок этих методов, что, как отмечалось выше, обычно сводится к проверке нормальности законов распределения переменных. [c.119]

Графически связь между плотностью вероятностей и вероятностью проиллюстрирована на рис. 17.2. В качестве примера взят нормальный закон распределения с параметрами среднее значение равно 2,4, дисперсия — 0,8. [c.452]

Решение уравнения Колмогорова (17.5) представляет собой нормальный закон распределения со следующими параметрами независимая переменная с математическим ожиданием равным [c.454]

После предварительной обработки статистического материала была принята гипотеза о нормальном законе распределения показателей фактической надежности, т.е. плотность вероятности [c.233]

Гипотеза о нормальном законе распределения проверялась по критерию Пирсона, подтвердившему ее. [c.233]

Все признаки и их совместные распределения должны подчиняться нормальному закону распределения. [c.114]

Конечно, принятые допущения могут представляться частично спорными, они действительно могут не соблюдаться для всех видов риска, но в общем они верно отражают общие закономерности изменения предпринимательского риска, опираются на естественную гипотезу, что прибыль как случайная величина подчинена нормальному или близкому к нормальному закону распределения. [c.178]

Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и а2, если ее плотность вероятности имеет вид [c.34]

Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис. 2.4). [c.34]

Нормальный закон распределения с параметрами а = О, [c.34]

Из второго свойства вытекает, в частности, правило трех сигм Если случайная величина X имеет нормальный закон распределения с параметрами аи а2, т.е. N(a o2 , то практически достоверно, что ее значения заключены в интервале (а — За, а + За). [c.35]

Двумерный (n-мерный) нормальный закон распределения [c.40]

Нормальный закон распределения n-мерной случайной величины (n-мерного случайного вектора) X = (Х, Х . Х ) характеризуется параметрами, задаваемыми вектором средних а = (a, ai. a и ковариационной матрицей X = (°у )пхп гДе